Click "Run Processing" to generate the image
Magellan Radar Demo - ML-Powered Surface Analysis | by Henrik Hargitai & Viktor Somogyi for HUN-REN / ESA
Processing...
Click: local patch analysis | Double-click: enlarge image
Click "Run Processing" to generate the image
Drag to move the ROI box. Drag corners to resize.
Position: X: 0, Y: 0
Size: 512 x 450 px
Size: 128-512 pixels (min-max)
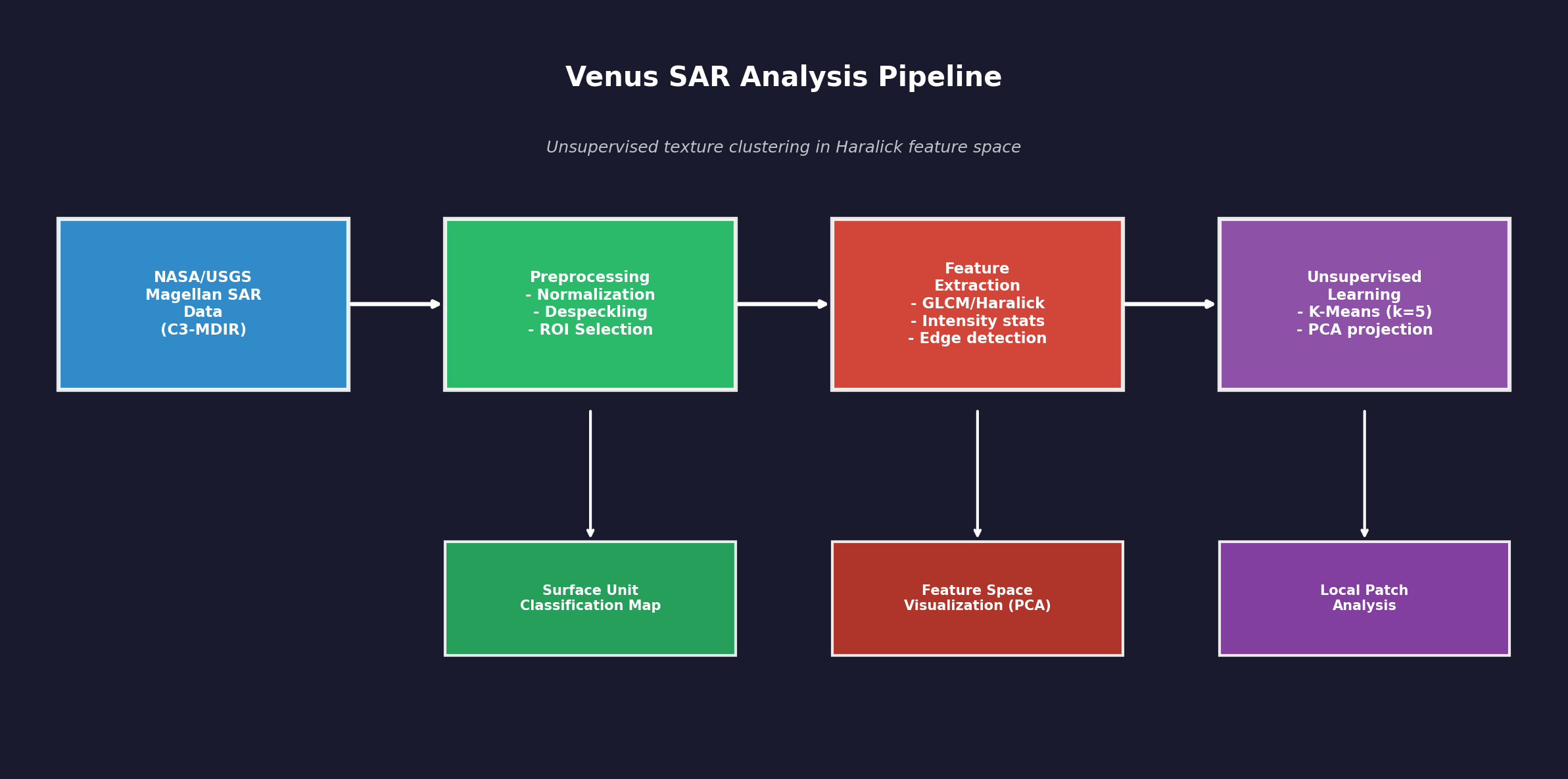
Data flow: SAR data from NASA/USGS Magellan mission is preprocessed (normalization, despeckling), then texture features are extracted using GLCM/Haralick methods. K-Means clustering groups similar texture patches into surface units. PCA projects the feature space to 2D for visualization.
This is unsupervised exploration - no geological labels are assigned. The tool proposes preliminary surface units based on texture similarity.
Loading 3D model...
Interactive 3D model of Venus surface. Use mouse to rotate, scroll to zoom.
This presentation was given at the Linux Foundation Amsterdam conference in the OpenSource AI/ML_DEV section. Viktor Somogyi presents the Venus SAR Exploratory Lab project.
The current web-based application of the Venus SAR Exploratory Lab is a lightweight, easily shareable, interactive demonstration and exploratory interface for NASA Magellan Synthetic Aperture Radar (SAR) data of Venus.
The long-term objective, however, is significantly more ambitious: the development of a supervised machine-learning model trained on annotated data, capable of more reliable and scientifically rigorous identification and analysis of planetary geological features.
At present, this complete system cannot be presented on the web in the same way, as the actual development environment involves orders of magnitude larger datasets (hundreds of gigabytes) and substantially higher computational requirements. The goal, nevertheless, is to make the results of the future, validated supervised pipeline presentable in a similarly transparent and interactive form.
Viktor Somogyi is the ML/AI engineer and lead developer of the project, while Henrik Hargitai, Ph.D. is a planetary geographer and geologist, contributing to the geological interpretation framework and scientific context.
The Venus SAR Exploratory Lab is a web-based interactive application designed to support exploratory analysis of Synthetic Aperture Radar (SAR) imagery acquired by the NASA Magellan spacecraft between 1990 and 1994.
Its purpose is to examine surface patterns on Venus using image processing and machine learning tools, in a way that is transparent, explainable, and suitable for educational use.
This application is not a geological classification system.
Its outputs are exploratory and hypothesis-generating, and all results require expert interpretation. The application does not assign geological labels (e.g., "this is definitely a lava flow") to detected patterns.
The application uses a widely adopted global Magellan mosaic published by the NASA Planetary Data System (PDS) and USGS Astrogeology:
The web application downloads the mosaic on first use and caches it locally.
SAR backscatter intensity is not an optical photograph. Pixel values represent radar signal backscatter, which may be influenced by surface roughness, slope, and viewing geometry (incidence angle). A general interpretation framework is:
SAR is not a camera: Unlike a photograph, this image wasn't made with light. SAR (Synthetic Aperture Radar) works by sending radio waves to the surface and measuring what bounces back. It's more like echolocation (how bats "see") than photography.
Why does this matter? In photos, we see color and shadows based on sunlight. In radar images, we see how much radio energy bounced back. This depends on three main things:
Geography application: Once you understand this, you can start "reading" the landscape. A bright ring might be a crater rim (rough, angled surface). A dark patch might be a smooth lava plain. Scientists use these patterns to understand Venus's geology without ever landing there.
The Venus SAR Exploratory Lab provides several processing modes. All modes operate on the same Region of Interest (ROI), allowing the user to view the same surface area through different analytical perspectives.
The normalized backscatter intensity image of the selected ROI, scaled to the 0-1 range. This serves as the reference for all other processing modes.
What you're seeing: This is a "photograph" of Venus taken not with light, but with radio waves. The Magellan spacecraft orbited Venus and sent radar signals down to the surface. When those signals bounced back, the spacecraft recorded them - that's what creates this image.
Why radar? Venus is covered by thick clouds that block visible light completely. Radar waves can pass through clouds, so this is the only way we can "see" the surface without landing on it.
How to read it: Bright areas = rough surfaces or slopes facing the spacecraft. Dark areas = smooth surfaces or areas in "radar shadow." Think of it like shining a flashlight on a textured wall - bumpy parts reflect more light back to you.
The computer science: The raw data is just numbers (pixel values). We normalize them to a 0-1 range so that 0 = darkest and 1 = brightest, making it easier for both humans and algorithms to work with the data consistently.
SAR imagery inherently contains speckle noise resulting from coherent interference. The system applies median filtering to reduce speckle, which can improve the stability of subsequent texture- and edge-based analyses, while potentially smoothing out some fine details.
The problem: Radar images have a grainy, "salt and pepper" look called speckle. This isn't real surface detail - it's noise created by the way radar waves interfere with each other. Imagine trying to hear someone talk in a room with echo - the echo isn't part of their voice, it's just interference.
The solution: We use a "median filter" - the computer looks at each pixel and its neighbors, sorts their values, and picks the middle one. This removes extreme bright or dark spots (the noise) while keeping real features.
Geography connection: Smoother images help us see actual landforms better - like distinguishing between a real volcanic feature and random radar noise. However, very small details might get smoothed away too, so there's always a trade-off.
Real-world analogy: It's like using noise-canceling headphones - they remove the unwanted background noise so you can hear the music (the real signal) more clearly.
The system computes Haralick texture metrics based on Gray-Level Co-occurrence Matrices (GLCM), using block-based analysis (e.g., 16x16 px). Extracted metrics (contrast, homogeneity, energy, correlation) are texture descriptors and do not identify geological units by themselves; however, they are useful for comparing surface patterns and supporting further exploratory analysis.
What is texture? Texture describes how "busy" or "smooth" an area looks. A field of grass has a different texture than a parking lot, even if they're the same color. On Venus, different geological regions have different textures.
How does the computer measure texture? The GLCM method asks: "If I'm looking at a pixel, what values do its neighbors usually have?" If neighbors are very different (high contrast), the area is rough/varied. If neighbors are similar (high homogeneity), the area is smooth/uniform.
The four measurements:
Geography connection: Different geological surfaces (lava flows, fractured terrain, plains) have characteristic textures. By measuring texture mathematically, we can start to distinguish between different types of terrain - though this alone can't tell us exactly what geological feature we're looking at.
Sobel and Canny operators highlight locations of strong local intensity change. This can be useful for visualizing structural transitions, but an important limitation is that not every detected edge represents a geological boundary; noise, shadowing, or processing artifacts may also produce edges.
What are edges? An edge is where brightness changes suddenly - like the border between a white wall and a dark door. In planetary images, edges might indicate cliffs, crater rims, lava flow boundaries, or fault lines.
How does edge detection work? The Sobel operator calculates how quickly brightness changes horizontally and vertically. Big changes = edges. The Canny detector refines this further, finding thin, connected edge lines.
Why two directions? Sobel X finds vertical edges (things that change left-to-right), Sobel Y finds horizontal edges (things that change top-to-bottom). Together they catch edges at any angle.
Geography connection: Linear features on Venus (fractures, ridges, flow boundaries) often appear as edges. However, radar shadows and noise can also create false edges, so scientists must interpret results carefully.
Computer science insight: Edge detection is fundamental to computer vision - it's used everywhere from self-driving cars (detecting road lanes) to medical imaging (finding tumor boundaries).
In this mode, the system samples patches (e.g., 32x32 px) from the ROI and computes feature vectors for each patch (mean, standard deviation, plus Haralick metrics), followed by K-Means clustering. The output represents unsupervised grouping of areas with similar texture, not geological unit identification. A PCA scatter plot is provided to visualize the structure of the feature space.
The big idea: Instead of a human looking at the image and saying "this area looks different from that one," we let the computer find groups automatically. This is called "unsupervised learning" - the computer learns patterns without being told what to look for.
How K-Means works: Imagine you have a pile of mixed candies and want to sort them into 5 groups by color. You'd put similar colors together. K-Means does the same thing, but instead of color, it groups image patches by their texture properties (the 6 numbers we measure for each patch).
What is PCA? Each patch has 6 measurements, which is hard to visualize (we can't draw in 6 dimensions!). PCA compresses these 6 numbers into 2 numbers while keeping the most important differences. This lets us plot the patches on a 2D scatter chart to see how they cluster.
Geography connection: Different terrain types (smooth plains, rough highlands, fractured zones) should have different textures and therefore fall into different clusters. However, one cluster doesn't mean "this is definitely lava" - it just means "these areas have similar texture properties."
Why 5 clusters? We chose 5 as a reasonable starting point. The real Venus surface might have more or fewer distinct terrain types in any given region. This is exploratory analysis, not definitive classification.
This mode does not perform classification. Instead, it highlights where texture properties change strongly over short spatial distances. After sliding-window feature extraction, a continuous 0-1 boundary likelihood map is generated based on feature-space distances between neighboring windows. High values indicate texture discontinuities, which may correspond to surface unit boundaries, but the output remains exploratory and interpretation-dependent.
The question we're asking: Where does the surface character change? If you're walking across a beach and suddenly the sand becomes rocky, that's a boundary. We're looking for similar transitions on Venus.
How it works: The computer slides a small window across the image. For each position, it measures the texture. Then it asks: "Is this window's texture very different from its neighbors?" If yes, we're probably at a boundary.
The heat map: The result is a probability map from 0 to 1. Bright/warm colors (close to 1) mean "texture changes a lot here" - likely a boundary. Dark/cool colors (close to 0) mean "texture is consistent" - probably the middle of a uniform region.
Geography connection: Geological unit boundaries (where lava flow meets older terrain, or where one rock type transitions to another) often show up as texture discontinuities. This can help scientists identify areas worth studying in more detail.
Important limitation: Not every texture change is a real geological boundary - some might be artifacts or gradual transitions. This tool highlights candidates for human expert review, not definitive boundaries.
Using a structure tensor approach, the system computes a local orientation field and an associated coherence/anisotropy metric (0 = isotropic, 1 = strongly directional). Visualization is performed using an HSV color scheme (hue: orientation, brightness: coherence), with an optional rose diagram. This mode is not a geological classification, but a visualization of directional fabric and confidence in the orientation estimate.
What are we looking for? Many geological features have a preferred direction - fault lines run parallel to each other, lava channels flow in one direction, ridges align along tectonic trends. This mode finds and visualizes those directions.
How it works: The "structure tensor" is a mathematical tool that looks at how brightness changes in all directions around each pixel. If changes are much stronger in one direction than others, that pixel has a clear orientation.
The color map explained:
The rose diagram: A circular histogram showing which directions are most common across the whole image. Peaks in the diagram indicate dominant structural orientations.
Geography connection: Tectonic forces create aligned features - parallel fractures, linear ridges, elongated volcanic structures. Seeing a consistent orientation across a region might indicate underlying geological processes that created aligned structures.
The "180° ambiguity": A line pointing northeast-southwest is the same line as one pointing southwest-northeast. The algorithm can't distinguish these, so orientations are reported in a range of only 180°, not 360°.
The system also includes a module that uses geometric and texture-based heuristics to mark potential candidates (e.g., circular and linear patterns, as well as patterns often discussed in Venus research).
These outputs are not validated geological identifications.
The documentation explicitly highlights potential false positives, parameter sensitivity, and the necessity of expert review.
What is this doing? This experimental feature tries to automatically find shapes that might be interesting geological features - like circles (possible craters or volcanic domes) or lines (possible fractures or ridges).
How does it work? The computer uses pattern recognition algorithms:
Why "candidates" not "discoveries"? The computer can find circles, but it can't know if a circle is a crater, a volcanic dome, or just a random pattern. Many "detections" are false positives - things that look like circles but aren't real geological features.
Geography context: Venus has unique features not found on Earth or Moon - coronae (large oval volcanic structures), arachnoids (features with radial fractures like spider legs), and tessera (highly deformed ancient terrain). This tool helps flag areas that might contain such features for human experts to examine.
The role of AI: This is "computer vision" - teaching computers to see patterns. But recognizing a pattern isn't the same as understanding what it means. That's why expert scientists must review every detection.
The Morphospace mode creates an interactive 3D visualization where each point represents a texture patch from the ROI. Similar textures cluster together in this abstract "feature space."
Important: The axes represent mathematical dimensions from UMAP dimensionality reduction, NOT physical coordinates or topography.
What is a "morphospace"? Imagine each small patch of the Venus surface as having a "personality" described by numbers - how bright it is, how rough, how textured. Morphospace is like a 3D map where similar personalities cluster together.
Why 3D? The original data has 8 dimensions (8 different measurements per patch). Humans can't visualize 8D, so we use math (UMAP algorithm) to squash it down to 3D while keeping similar things close together.
What can you learn? Patches that cluster together likely represent similar surface types - maybe all smooth plains, or all rough volcanic terrain. The colors help you see these natural groupings.
Users can select a region of interest on the global mosaic (default size e.g. 1024x1024 px). All processing modes operate on the selected ROI.
By clicking on a processed image, the system extracts a 128x128 px neighborhood and displays it in multiple views (raw, despeckled, edges, and - if clustering has been run - cluster assignment).
Each mode includes a step-by-step processing log with short explanations and the actual Python code snippets executed. This supports transparency, educational use, and debugging.
Why ROI selection matters: The full Venus radar map is huge - about 170 megabytes. Processing the entire planet at once would be slow and overwhelming. Instead, you pick a "Region of Interest" (ROI) - a smaller area to study in detail. Think of it like zooming in on Google Maps to see your neighborhood instead of the whole Earth.
Click to explore: When you click on the processed image, the system shows you a close-up of that exact spot with multiple analysis views. This is like having a magnifying glass that not only zooms in but also applies different filters to help you understand what you're looking at.
Why show the code? The Processing Log shows the actual Python code being executed. This serves several purposes:
Computer science connection: This interactive approach is called "exploratory data analysis" - instead of running one fixed analysis, you can dynamically explore different areas and apply different methods, building intuition about the data before forming hypotheses.
Key documented limitations include:
Ez az előadás a Linux Foundation amszterdami konferenciáján hangzott el az OpenSource AI/ML_DEV szekcióban. Somogyi Viktor mutatja be a Vénusz SAR Kutató Laboratórium projektet.
A Vénusz SAR Kutató Laboratórium jelenlegi webes alkalmazása egy könnyű, könnyen megosztható, interaktív bemutató és feltáró felület a NASA Magellan szintetikus apertúrájú radar (SAR) adataihoz a Vénuszról.
A hosszú távú cél azonban lényegesen ambiciózusabb: egy annotált adatokon betanított felügyelt gépi tanulási modell fejlesztése, amely megbízhatóbban és tudományosan megalapozottabban képes azonosítani és elemezni a bolygógeológiai jellemzőket.
Jelenleg ez a teljes rendszer nem mutatható be hasonló módon a weben, mivel a tényleges fejlesztési környezet nagyságrendekkel nagyobb adathalmazokat (több száz gigabájt) és lényegesen nagyobb számítási kapacitást igényel. A cél mindazonáltal az, hogy a jövőbeli, validált felügyelt feldolgozási lánc eredményei hasonlóan átlátható és interaktív formában legyenek bemutathatók.
Somogyi Viktor a projekt ML/AI mérnöke és vezető fejlesztője, míg Dr. Hargitai Henrik bolygókutató geográfus és geológus, aki a geológiai értelmezési keretrendszerhez és a tudományos kontextushoz járul hozzá.
A Vénusz SAR Kutató Laboratórium egy webalapú interaktív alkalmazás, amelyet a NASA Magellan űrszonda által 1990 és 1994 között készített szintetikus apertúrájú radar (SAR) felvételek feltáró elemzésének támogatására terveztek.
Célja a Vénusz felszíni mintázatainak vizsgálata képfeldolgozó és gépi tanulási eszközökkel, átlátható, magyarázható és oktatási célokra is alkalmas módon.
Ez az alkalmazás nem geológiai osztályozási rendszer.
Az eredmények feltáró jellegűek és hipotézis-generálók, minden eredmény szakértői értelmezést igényel. Az alkalmazás nem rendel geológiai címkéket (pl. "ez biztosan lávafolyás") az észlelt mintázatokhoz.
Az alkalmazás a NASA Planetary Data System (PDS) és az USGS Astrogeology által közzétett, széles körben használt globális Magellan mozaikot használja:
A webalkalmazás első használatkor letölti a mozaikot és helyben gyorsítótárazza.
A SAR visszaverődési intenzitás nem optikai fénykép. A pixelértékek a radarjel visszaverődését reprezentálják, amelyet a felszín érdessége, lejtése és a megfigyelési geometria (beesési szög) befolyásolhat. Általános értelmezési keretrendszer:
A SAR nem fényképezőgép: A hagyományos fényképektől eltérően ez a kép nem fénnyel készült. A SAR (szintetikus apertúrájú radar) úgy működik, hogy rádióhullámokat küld a felszínre és méri, mi verődik vissza. Inkább hasonlít a denevérek echolokációjához, mint a fényképezéshez.
Miért fontos ez? A fényképeken a színeket és árnyékokat a napfény alapján látjuk. A radarképeken azt látjuk, mennyi rádióenergia verődött vissza. Ez három fő dologtól függ:
Földrajzi alkalmazás: Ha ezt megérted, elkezdheted "olvasni" a tájat. Egy világos gyűrű lehet kráterperem (érdes, döntött felszín). Egy sötét folt lehet sima lávasíkság. A tudósok ezeket a mintázatokat használják a Vénusz geológiájának megértéséhez anélkül, hogy valaha is leszálltak volna ott.
A Vénusz SAR Kutató Laboratórium több feldolgozási módot kínál. Minden mód ugyanazon az érdeklődési régión (ROI) működik, lehetővé téve a felhasználónak, hogy ugyanazt a felszíni területet különböző elemzési perspektívákból tekintse meg.
A kiválasztott ROI normalizált visszaverődési intenzitásképe, 0-1 tartományra skálázva. Ez szolgál referenciaként minden más feldolgozási módhoz.
Amit látsz: Ez egy "fénykép" a Vénuszról, de nem fénnyel, hanem rádióhullámokkal készült. A Magellan űrszonda a Vénusz körül keringett és radarjeleket küldött a felszínre. Amikor ezek a jelek visszaverődtek, az űrszonda rögzítette őket - ez hozza létre a képet.
Miért radar? A Vénuszt sűrű felhők borítják, amelyek teljesen blokkolják a látható fényt. A radarhullámok áthaladnak a felhőkön, így ez az egyetlen mód, ahogy "láthatjuk" a felszínt leszállás nélkül.
Hogyan olvasd: Világos területek = érdes felszínek vagy az űrszonda felé néző lejtők. Sötét területek = sima felszínek vagy "radar-árnyékban" lévő területek.
A SAR képek természetüknél fogva tartalmaznak pöttyös zajt a koherens interferencia miatt. A rendszer mediánszűrést alkalmaz a pöttyösség csökkentésére, ami javíthatja a későbbi textúra- és él-alapú elemzések stabilitását, miközben potenciálisan kisimíthat néhány finom részletet.
A probléma: A radarképeknek szemcsés, "só-és-bors" kinézete van, amit pöttyösségnek nevezünk. Ez nem valódi felszíni részlet - ez zaj, amit a radarhullámok egymással való interferenciája hoz létre.
A megoldás: "Mediánszűrőt" használunk - a számítógép minden pixelt és szomszédait nézi, sorba rendezi értékeiket, és a középsőt választja. Ez eltávolítja a szélsőségesen világos vagy sötét pontokat (a zajt), miközben megtartja a valódi jellemzőket.
A rendszer Haralick textúra-metrikákat számít Gray-Level Co-occurrence Matrices (GLCM) alapján, blokk-alapú elemzéssel (pl. 16x16 px). A kinyert metrikák (kontraszt, homogenitás, energia, korreláció) textúra-leírók, és önmagukban nem azonosítanak geológiai egységeket; azonban hasznosak a felszíni minták összehasonlításához és a további feltáró elemzés támogatásához.
Mi a textúra? A textúra azt írja le, mennyire "zsúfolt" vagy "sima" egy terület kinézete. A fűmezőnek más textúrája van, mint a parkolónak, még ha azonos színűek is. A Vénuszon a különböző geológiai régióknak különböző textúrájuk van.
A négy mérés:
A Sobel és Canny operátorok kiemelik az erős lokális intenzitásváltozás helyeit. Ez hasznos lehet a szerkezeti átmenetek vizualizálásához, de fontos korlát, hogy nem minden detektált él jelent geológiai határt; zaj, árnyékolás vagy feldolgozási műtermékek is éleket produkálhatnak.
Mik az élek? Az él ott van, ahol a fényesség hirtelen változik - mint a fehér fal és a sötét ajtó közötti határ. Bolygóképeken az élek sziklákat, kráterperemeket, lávafolyás-határokat vagy törésvonalakat jelezhetnek.
Hogyan működik az éldetektálás? A Sobel operátor kiszámítja, milyen gyorsan változik a fényesség vízszintesen és függőlegesen. Nagy változások = élek.
Ebben a módban a rendszer régiókat (pl. 32x32 px) mintavételez a ROI-ból és jellemzővektorokat számít minden régióhoz (átlag, szórás, plusz Haralick metrikák), majd K-közép klaszterezést alkalmaz. Az eredmény hasonló textúrájú területek felügyelet nélküli csoportosítását reprezentálja, nem geológiai egység-azonosítást. PCA szórásdiagram segíti a jellemzőtér struktúrájának vizualizálását.
A nagy ötlet: Ahelyett, hogy ember nézné a képet és mondaná "ez a terület másnak tűnik, mint az", hagyjuk, hogy a számítógép automatikusan találja meg a csoportokat. Ezt "felügyelet nélküli tanulásnak" hívják.
Hogyan működik a K-közép: Képzeld el, hogy van egy kupac kevert cukorka és 5 csoportba akarod válogatni szín szerint. A hasonló színeket összeraknád. A K-közép ugyanezt teszi, de szín helyett a képrégiókat textúra-tulajdonságaik alapján csoportosítja.
Mi a PCA? Minden régiónak 6 mérése van, amit nehéz vizualizálni. A PCA (főkomponens-analízis) tömöríti ezt a 6 számot 2 számra, miközben megőrzi a legfontosabb különbségeket. Ez lehetővé teszi a régiók 2D pontdiagramon való ábrázolását.
Ez a mód nem végez osztályozást. Ehelyett kiemeli, ahol a textúra-tulajdonságok erősen változnak rövid térbeli távolságokon. Csúszóablakos jellemző-kivonás után folytonos 0-1 határ-valószínűségi térkép generálódik a szomszédos ablakok közötti jellemzőtér-távolságok alapján.
A kérdés, amit felteszünk: Hol változik meg a felszín jellege? Ha sétálsz a strandon és hirtelen a homok sziklássá válik, az határ. Hasonló átmeneteket keresünk a Vénuszon.
A hőtérkép: Az eredmény 0-tól 1-ig terjedő valószínűségi térkép. Világos/meleg színek (1-hez közel) azt jelentik: "a textúra sokat változik itt" - valószínűleg határ. Sötét/hideg színek (0-hoz közel) azt jelentik: "a textúra konzisztens" - valószínűleg egyenletes régió közepe.
Struktúratenzor megközelítéssel a rendszer lokális orientációs mezőt és kapcsolódó koherencia/anizotrópia metrikát számít (0 = izotróp, 1 = erősen irányított). A vizualizáció HSV színsémával történik (árnyalat: orientáció, fényesség: koherencia), opcionális rózsa diagrammal.
Mit keresünk? Sok geológiai jellemzőnek van preferált iránya - a törésvonalak párhuzamosan futnak, a lávacsatornák egy irányba folynak. Ez a mód megtalálja és vizualizálja ezeket az irányokat.
A színtérkép magyarázata:
A rózsa diagram: Körkörös hisztogram, ami megmutatja, mely irányok a leggyakoribbak a képen. A csúcsok a domináns szerkezeti orientációkat jelzik.
A rendszer tartalmaz egy modult is, amely geometriai és textúra-alapú heurisztikákat használ potenciális jelöltek megjelölésére (pl. körkörös és lineáris minták, valamint a Vénusz-kutatásban gyakran tárgyalt minták).
Ezek az eredmények nem validált geológiai azonosítások.
A dokumentáció kifejezetten kiemeli a lehetséges téves pozitívokat, a paraméter-érzékenységet és a szakértői felülvizsgálat szükségességét.
Mit csinál ez? Ez a kísérleti funkció megpróbál automatikusan olyan formákat találni, amelyek érdekes geológiai jellemzők lehetnek - mint körök (lehetséges kráterek vagy vulkáni dómok) vagy vonalak (lehetséges törések vagy gerincek).
Miért "jelöltek" és nem "felfedezések"? A számítógép köröket talál, de nem tudhatja, hogy egy kör kráter, vulkáni dóm vagy csak véletlenszerű minta. Sok "detektálás" téves pozitív - olyan dolgok, amik körnek tűnnek, de nem valódi geológiai jellemzők.
A Morfoszféra mód interaktív 3D vizualizációt hoz létre, ahol minden pont egy textúra-régiót képvisel a ROI-ból. A hasonló textúrák csoportosulnak ebben az absztrakt "jellemzőtérben."
Fontos: A tengelyek matematikai dimenziókat képviselnek a UMAP dimenziócsökkentésből, NEM fizikai koordinátákat vagy topográfiát.
Mi az a "morfoszféra"? Képzeld el, hogy a Vénusz felszínének minden kis darabjának van egy "személyisége", amit számok írnak le - milyen fényes, milyen érdes, milyen textúrájú. A morfoszféra olyan, mint egy 3D-s térkép, ahol a hasonló személyiségek csoportosulnak.
Miért 3D? Az eredeti adatnak 8 dimenziója van (8 különböző mérés patchenként). Az emberek nem tudnak 8D-t elképzelni, ezért matematikát (UMAP algoritmus) használunk, hogy 3D-re tömörítsük, miközben a hasonló dolgok közel maradnak egymáshoz.
Mit tanulhatsz belőle? Az együtt csoportosuló patchek valószínűleg hasonló felszíntípusokat képviselnek - talán mind sima síkságok, vagy mind érdes vulkáni terep. A színek segítenek látni ezeket a természetes csoportosulásokat.
A felhasználók kiválaszthatnak egy érdeklődési régiót a globális mozaikon (alapértelmezett méret pl. 1024x1024 px). Minden feldolgozási mód a kiválasztott ROI-n működik.
A feldolgozott képre kattintva a rendszer kinyeri a 128x128 px-es környezetet és több nézetben jeleníti meg (nyers, zajszűrt, élek, és - ha klaszterezés futott - klaszter-hozzárendelés).
Minden mód tartalmaz lépésről-lépésre feldolgozási naplót rövid magyarázatokkal és a ténylegesen végrehajtott Python kódrészletekkel. Ez támogatja az átláthatóságot, az oktatási felhasználást és a hibakeresést.
Miért fontos a ROI kiválasztás: A teljes Vénusz radartérkép hatalmas - kb. 170 megabájt. Az egész bolygó egyszerre feldolgozása lassú és túlterhelő lenne. Ehelyett kiválasztasz egy "érdeklődési régiót" (ROI) - egy kisebb területet a részletes tanulmányozáshoz.
Kattints a felfedezéshez: Amikor rákattintasz a feldolgozott képre, a rendszer megmutatja az adott pont közeli felvételét több elemzési nézetben.
Miért mutatjuk a kódot? A Feldolgozási napló mutatja a ténylegesen végrehajtott Python kódot. Ez többféle célt szolgál: átláthatóság, oktatás és reprodukálhatóság.
Főbb dokumentált korlátozások:
This developer guide provides copy-paste ready Python code examples for implementing the image processing and machine learning methods used in the Venus SAR Exploratory Lab.
SAR Image (GeoTIFF)
│
├── Preprocessing
│ ├── Normalization (0-1 range)
│ └── Speckle reduction (median filter)
│
├── Feature Extraction
│ ├── GLCM Haralick textures
│ ├── Edge detection (Sobel, Canny)
│ └── Structure tensor (orientation)
│
└── ML Analysis
├── K-Means clustering
├── PCA visualization
└── UMAP embeddingimport numpy as np
import matplotlib.pyplot as plt
from skimage import io, filters, feature, exposure
from skimage.filters import median, sobel_h, sobel_v
from skimage.morphology import disk
from skimage.feature import graycomatrix, graycoprops, canny
from sklearn.cluster import MiniBatchKMeans
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import umapThe Venus Magellan C3-MDIR Global Mosaic is publicly available from NASA/USGS:
# Data URL
url = "https://planetarymaps.usgs.gov/mosaic/Venus_Magellan_C3-MDIR_Global_Mosaic_2025m.tif"
# Download and load using requests + PIL/tifffile
import requests
from PIL import Image
import io
response = requests.get(url)
image = Image.open(io.BytesIO(response.content))
data = np.array(image)
# Or use tifffile for GeoTIFF
import tifffile
data = tifffile.imread('Venus_Magellan_C3-MDIR_Global_Mosaic_2025m.tif')
# Normalize to 0-1 range
data = data.astype(np.float32)
data = (data - data.min()) / (data.max() - data.min())Basic preprocessing to normalize SAR amplitude values:
def process_raw(image: np.ndarray) -> np.ndarray:
"""
Normalize SAR image to 0-1 range.
Parameters:
image: 2D numpy array of SAR backscatter values
Returns:
Normalized image (float32, range 0-1)
"""
img = image.astype(np.float32)
img_min, img_max = img.min(), img.max()
if img_max - img_min > 0:
normalized = (img - img_min) / (img_max - img_min)
else:
normalized = np.zeros_like(img)
return normalized
# Visualization
fig, ax = plt.subplots(figsize=(10, 10))
im = ax.imshow(normalized_image, cmap='gray', vmin=0, vmax=1)
plt.colorbar(im, label='Normalized Radar Backscatter')
ax.set_title('Venus Magellan SAR - Raw')
plt.show()SAR images contain coherent speckle noise. Median filtering reduces speckle while preserving edges:
from skimage.filters import median
from skimage.morphology import disk
def process_despeckle(image: np.ndarray, radius: int = 3) -> np.ndarray:
"""
Apply median filter for speckle reduction.
Parameters:
image: Normalized SAR image (0-1 range)
radius: Radius of circular structuring element (default: 3)
Returns:
Despeckled image
"""
despeckled = median(image, disk(radius))
return despeckled
# Compare original vs despeckled
fig, axes = plt.subplots(1, 2, figsize=(14, 7))
axes[0].imshow(original, cmap='gray')
axes[0].set_title('Original SAR Image')
axes[1].imshow(despeckled, cmap='gray')
axes[1].set_title(f'Despeckled (radius={radius})')
plt.tight_layout()Gray-Level Co-occurrence Matrix (GLCM) extracts texture descriptors:
from skimage.feature import graycomatrix, graycoprops
def compute_glcm_features(block: np.ndarray, levels: int = 16) -> dict:
"""
Compute GLCM Haralick texture features for an image block.
Parameters:
block: 2D image block (uint8, 0-255 or scaled to levels)
levels: Number of gray levels for GLCM
Returns:
Dictionary with contrast, homogeneity, energy, correlation
"""
# Scale to desired levels
block_scaled = ((block - block.min()) /
(block.max() - block.min() + 1e-8) * (levels-1)).astype(np.uint8)
# Compute GLCM
glcm = graycomatrix(block_scaled,
distances=[1],
angles=[0, np.pi/4, np.pi/2, 3*np.pi/4],
levels=levels,
symmetric=True,
normed=True)
# Extract Haralick features (average over angles)
features = {
'contrast': graycoprops(glcm, 'contrast').mean(),
'homogeneity': graycoprops(glcm, 'homogeneity').mean(),
'energy': graycoprops(glcm, 'energy').mean(),
'correlation': graycoprops(glcm, 'correlation').mean()
}
return features
def compute_texture_maps(image: np.ndarray, block_size: int = 16) -> dict:
"""
Compute texture feature maps for entire image using sliding blocks.
Parameters:
image: Normalized SAR image
block_size: Size of analysis blocks in pixels
Returns:
Dictionary of 2D texture maps
"""
h, w = image.shape
h_blocks, w_blocks = h // block_size, w // block_size
# Initialize maps
contrast_map = np.zeros((h_blocks, w_blocks))
homogeneity_map = np.zeros((h_blocks, w_blocks))
energy_map = np.zeros((h_blocks, w_blocks))
correlation_map = np.zeros((h_blocks, w_blocks))
img_uint8 = (image * 255).astype(np.uint8)
for i in range(h_blocks):
for j in range(w_blocks):
block = img_uint8[i*block_size:(i+1)*block_size,
j*block_size:(j+1)*block_size]
if block.max() > block.min():
features = compute_glcm_features(block)
contrast_map[i, j] = features['contrast']
homogeneity_map[i, j] = features['homogeneity']
energy_map[i, j] = features['energy']
correlation_map[i, j] = features['correlation']
return {
'contrast': contrast_map,
'homogeneity': homogeneity_map,
'energy': energy_map,
'correlation': correlation_map
}Sobel gradients and Canny edge detection for structural analysis:
from skimage.filters import sobel_h, sobel_v
from skimage.feature import canny
def process_edges(image: np.ndarray, sigma: float = 2.0) -> dict:
"""
Compute edge detection using Sobel and Canny operators.
Parameters:
image: Normalized SAR image
sigma: Gaussian smoothing for Canny
Returns:
Dictionary with gradients and edge maps
"""
# Sobel gradients
grad_x = sobel_h(image) # Horizontal gradient
grad_y = sobel_v(image) # Vertical gradient
# Gradient magnitude
gradient_magnitude = np.sqrt(grad_x**2 + grad_y**2)
# Canny edge detection
edges = canny(image, sigma=sigma, low_threshold=0.05, high_threshold=0.15)
return {
'grad_x': grad_x,
'grad_y': grad_y,
'magnitude': gradient_magnitude,
'edges': edges
}
# Visualization
fig, axes = plt.subplots(2, 2, figsize=(12, 12))
axes[0,0].imshow(image, cmap='gray')
axes[0,0].set_title('Original')
axes[0,1].imshow(result['grad_x'], cmap='RdBu')
axes[0,1].set_title('Sobel X (horizontal edges)')
axes[1,0].imshow(result['grad_y'], cmap='RdBu')
axes[1,0].set_title('Sobel Y (vertical edges)')
axes[1,1].imshow(result['edges'], cmap='gray')
axes[1,1].set_title('Canny Edges')Unsupervised texture clustering with PCA visualization:
from sklearn.cluster import MiniBatchKMeans
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
def extract_patch_features(patch: np.ndarray) -> np.ndarray:
"""
Extract 6D feature vector from a patch.
Features: [mean, std, contrast, homogeneity, energy, correlation]
"""
# Intensity statistics
mean_i = patch.mean()
std_i = patch.std()
# GLCM features
patch_uint8 = (patch * 255).astype(np.uint8)
patch_scaled = ((patch_uint8 - patch_uint8.min()) /
(patch_uint8.max() - patch_uint8.min() + 1e-8) * 15).astype(np.uint8)
glcm = graycomatrix(patch_scaled, distances=[1], angles=[0],
levels=16, symmetric=True, normed=True)
contrast = graycoprops(glcm, 'contrast')[0, 0]
homogeneity = graycoprops(glcm, 'homogeneity')[0, 0]
energy = graycoprops(glcm, 'energy')[0, 0]
correlation = graycoprops(glcm, 'correlation')[0, 0]
return np.array([mean_i, std_i, contrast, homogeneity, energy, correlation])
def cluster_surface_units(image: np.ndarray,
patch_size: int = 32,
step: int = 16,
n_clusters: int = 5) -> dict:
"""
Perform K-Means clustering on texture patches.
Parameters:
image: Normalized SAR image
patch_size: Size of patches (pixels)
step: Stride between patches
n_clusters: Number of clusters
Returns:
Dictionary with cluster map, labels, and PCA coordinates
"""
h, w = image.shape
patches = []
positions = []
# Sample patches
for y in range(0, h - patch_size, step):
for x in range(0, w - patch_size, step):
patch = image[y:y+patch_size, x:x+patch_size]
patches.append(patch)
positions.append((y, x))
# Extract features
features = np.array([extract_patch_features(p) for p in patches])
# Standardize
scaler = StandardScaler()
features_scaled = scaler.fit_transform(features)
# K-Means clustering
kmeans = MiniBatchKMeans(n_clusters=n_clusters, random_state=42)
labels = kmeans.fit_predict(features_scaled)
# PCA for visualization
pca = PCA(n_components=2)
features_2d = pca.fit_transform(features_scaled)
# Create cluster map
cluster_map = np.zeros((h, w))
for idx, (y, x) in enumerate(positions):
cluster_map[y:y+patch_size, x:x+patch_size] = labels[idx]
return {
'cluster_map': cluster_map,
'labels': labels,
'features_2d': features_2d,
'positions': positions,
'kmeans': kmeans,
'scaler': scaler,
'pca': pca
}Detect boundaries between texture regions using feature-space gradients:
from scipy.ndimage import gaussian_filter
from skimage.transform import resize
def compute_boundary_map(image: np.ndarray,
window_size: int = 32,
step: int = 16) -> np.ndarray:
"""
Compute boundary probability based on texture discontinuity.
Parameters:
image: Normalized SAR image
window_size: Analysis window size
step: Window stride
Returns:
Boundary probability map (0-1)
"""
h, w = image.shape
n_y = (h - window_size) // step + 1
n_x = (w - window_size) // step + 1
# Extract features for each window
feature_grid = np.zeros((n_y, n_x, 6))
for i in range(n_y):
for j in range(n_x):
y, x = i * step, j * step
window = image[y:y+window_size, x:x+window_size]
feature_grid[i, j] = extract_patch_features(window)
# Standardize features
features_flat = feature_grid.reshape(-1, 6)
scaler = StandardScaler()
features_scaled = scaler.fit_transform(features_flat)
feature_grid_scaled = features_scaled.reshape(n_y, n_x, 6)
# Compute boundary scores (distance to neighbors)
boundary_scores = np.zeros((n_y, n_x))
neighbors = [(-1, 0), (1, 0), (0, -1), (0, 1)]
for i in range(n_y):
for j in range(n_x):
feat = feature_grid_scaled[i, j]
distances = []
for dy, dx in neighbors:
ni, nj = i + dy, j + dx
if 0 <= ni < n_y and 0 <= nj < n_x:
neighbor_feat = feature_grid_scaled[ni, nj]
dist = np.linalg.norm(feat - neighbor_feat)
distances.append(dist)
if distances:
boundary_scores[i, j] = np.mean(distances)
# Normalize to 0-1
if boundary_scores.max() > boundary_scores.min():
boundary_scores = (boundary_scores - boundary_scores.min()) / \
(boundary_scores.max() - boundary_scores.min())
# Upsample and smooth
boundary_map = resize(boundary_scores, image.shape, order=1)
boundary_map = gaussian_filter(boundary_map, sigma=1.5)
return boundary_mapCompute dominant structural orientation using the structure tensor:
from skimage.filters import scharr_h, scharr_v
from scipy.ndimage import gaussian_filter
import matplotlib.colors as mcolors
def compute_orientation(image: np.ndarray,
sigma: float = 2.0) -> dict:
"""
Compute dominant orientation using structure tensor.
Parameters:
image: Normalized SAR image
sigma: Smoothing for structure tensor
Returns:
Dictionary with orientation, coherence, and visualization
"""
# Despeckle first
image_smooth = median(image, disk(2))
# Compute gradients (Scharr for better rotation invariance)
Ix = scharr_h(image_smooth)
Iy = scharr_v(image_smooth)
# Structure tensor components with smoothing
Jxx = gaussian_filter(Ix * Ix, sigma=sigma)
Jyy = gaussian_filter(Iy * Iy, sigma=sigma)
Jxy = gaussian_filter(Ix * Iy, sigma=sigma)
# Orientation angle
theta = 0.5 * np.arctan2(2 * Jxy, Jxx - Jyy)
# Eigenvalues for coherence
sqrt_term = np.sqrt((Jxx - Jyy)**2 + 4 * Jxy**2)
lambda1 = 0.5 * (Jxx + Jyy + sqrt_term)
lambda2 = 0.5 * (Jxx + Jyy - sqrt_term)
# Coherence (anisotropy measure)
epsilon = 1e-10
coherence = (lambda1 - lambda2) / (lambda1 + lambda2 + epsilon)
# Mask low-energy regions
energy = lambda1 + lambda2
threshold = np.percentile(energy, 10)
mask = energy > threshold
coherence_masked = coherence * mask
# HSV visualization: Hue=orientation, Value=coherence
hue = (theta + np.pi/2) / np.pi # Map to [0, 1]
sat = np.ones_like(hue)
val = coherence_masked
hsv = np.stack([hue, sat, val], axis=-1)
rgb = mcolors.hsv_to_rgb(hsv)
return {
'theta': theta,
'coherence': coherence_masked,
'rgb': rgb
}Create a 3D morphospace visualization using UMAP dimensionality reduction:
import umap
from skimage.feature import canny
def extract_8d_features(patch: np.ndarray) -> np.ndarray:
"""
Extract 8D feature vector for morphospace analysis.
Features: [mean, std, contrast, homogeneity, energy, entropy,
edge_density, orientation_coherence]
"""
# Basic statistics
mean_i = patch.mean()
std_i = patch.std()
# GLCM features
patch_uint8 = (patch * 255).astype(np.uint8)
patch_scaled = ((patch_uint8 - patch_uint8.min()) /
(patch_uint8.max() - patch_uint8.min() + 1e-8) * 15).astype(np.uint8)
glcm = graycomatrix(patch_scaled, distances=[1], angles=[0],
levels=16, symmetric=True, normed=True)
contrast = graycoprops(glcm, 'contrast')[0, 0]
homogeneity = graycoprops(glcm, 'homogeneity')[0, 0]
energy = graycoprops(glcm, 'energy')[0, 0]
# Entropy
glcm_flat = glcm[:, :, 0, 0].flatten()
glcm_flat = glcm_flat[glcm_flat > 0]
entropy = -np.sum(glcm_flat * np.log2(glcm_flat + 1e-10))
# Edge density
edges = canny(patch, sigma=1.5)
edge_density = edges.mean()
# Orientation coherence
Ix = sobel_h(patch)
Iy = sobel_v(patch)
Jxx = gaussian_filter(Ix * Ix, sigma=1.5)
Jyy = gaussian_filter(Iy * Iy, sigma=1.5)
Jxy = gaussian_filter(Ix * Iy, sigma=1.5)
sqrt_term = np.sqrt((Jxx - Jyy)**2 + 4 * Jxy**2)
lambda1 = 0.5 * (Jxx + Jyy + sqrt_term)
lambda2 = 0.5 * (Jxx + Jyy - sqrt_term)
coherence = ((lambda1 - lambda2) / (lambda1 + lambda2 + 1e-10)).mean()
return np.array([mean_i, std_i, contrast, homogeneity,
energy, entropy, edge_density, coherence])
def create_morphospace(image: np.ndarray,
patch_size: int = 64,
step: int = 32,
n_clusters: int = 5) -> dict:
"""
Create 3D morphospace using UMAP embedding.
Parameters:
image: Normalized SAR image
patch_size: Patch size for feature extraction
step: Stride between patches
n_clusters: Number of K-Means clusters
Returns:
Dictionary with 3D coordinates, features, and clusters
"""
h, w = image.shape
patches = []
positions = []
for y in range(0, h - patch_size, step):
for x in range(0, w - patch_size, step):
patch = image[y:y+patch_size, x:x+patch_size]
patches.append(patch)
positions.append((y, x))
# Extract 8D features
features = np.array([extract_8d_features(p) for p in patches])
# Standardize
scaler = StandardScaler()
features_scaled = scaler.fit_transform(features)
# UMAP to 3D
reducer = umap.UMAP(n_components=3,
n_neighbors=15,
min_dist=0.1,
metric='euclidean',
random_state=42)
embedding_3d = reducer.fit_transform(features_scaled)
# K-Means clustering
kmeans = MiniBatchKMeans(n_clusters=n_clusters, random_state=42)
labels = kmeans.fit_predict(features_scaled)
return {
'embedding': embedding_3d,
'features': features,
'labels': labels,
'positions': positions,
'patches': patches
}
# Interactive 3D visualization with Plotly
import plotly.graph_objects as go
def plot_morphospace_3d(result: dict):
fig = go.Figure(data=[go.Scatter3d(
x=result['embedding'][:, 0],
y=result['embedding'][:, 1],
z=result['embedding'][:, 2],
mode='markers',
marker=dict(
size=4,
color=result['labels'],
colorscale='Viridis',
opacity=0.8
),
text=[f'Cluster {l+1}' for l in result['labels']]
)])
fig.update_layout(
title='Venus SAR Texture Morphospace',
scene=dict(
xaxis_title='UMAP 1',
yaxis_title='UMAP 2',
zaxis_title='UMAP 3'
)
)
return figPython dependencies for running all processing modes:
# requirements.txt
numpy>=1.21.0
scipy>=1.7.0
scikit-image>=0.19.0
scikit-learn>=1.0.0
matplotlib>=3.5.0
umap-learn>=0.5.0
plotly>=5.0.0
Pillow>=9.0.0
tifffile>=2022.0.0
requests>=2.27.0pip install -r requirements.txt
Ez a fejlesztői útmutató másolásra kész Python kódpéldákat tartalmaz a Venus SAR Exploratory Lab-ban használt képfeldolgozási és gépi tanulási módszerek implementálásához.
SAR Kép (GeoTIFF)
│
├── Előfeldolgozás
│ ├── Normalizálás (0-1 tartomány)
│ └── Pöttyösség-csökkentés (medián szűrő)
│
├── Jellemző Kinyerés
│ ├── GLCM Haralick textúrák
│ ├── Éldetektálás (Sobel, Canny)
│ └── Struktúra tenzor (orientáció)
│
└── ML Elemzés
├── K-közép klaszterezés
├── PCA vizualizáció
└── UMAP beágyazásA Venus Magellan C3-MDIR Globális Mozaik nyilvánosan elérhető a NASA/USGS szervereiről:
# Adat URL
url = "https://planetarymaps.usgs.gov/mosaic/Venus_Magellan_C3-MDIR_Global_Mosaic_2025m.tif"
# Letöltés és betöltés requests + PIL/tifffile használatával
import requests
from PIL import Image
import io
response = requests.get(url)
image = Image.open(io.BytesIO(response.content))
data = np.array(image)
# Vagy tifffile használata GeoTIFF-hez
import tifffile
data = tifffile.imread('Venus_Magellan_C3-MDIR_Global_Mosaic_2025m.tif')
# Normalizálás 0-1 tartományra
data = data.astype(np.float32)
data = (data - data.min()) / (data.max() - data.min())Alapvető előfeldolgozás a SAR amplitúdó értékek normalizálásához:
def process_raw(image: np.ndarray) -> np.ndarray:
"""
SAR kép normalizálása 0-1 tartományra.
Paraméterek:
image: 2D numpy tömb SAR visszaverődési értékekkel
Visszatérési érték:
Normalizált kép (float32, 0-1 tartomány)
"""
img = image.astype(np.float32)
img_min, img_max = img.min(), img.max()
if img_max - img_min > 0:
normalized = (img - img_min) / (img_max - img_min)
else:
normalized = np.zeros_like(img)
return normalized
# Vizualizáció
fig, ax = plt.subplots(figsize=(10, 10))
im = ax.imshow(normalized_image, cmap='gray', vmin=0, vmax=1)
plt.colorbar(im, label='Normalizált radar visszaverődés')
ax.set_title('Venus Magellan SAR - Nyers')
plt.show()A SAR képek koherens pöttyösséget (speckle) tartalmaznak. A mediánszűrő csökkenti a zajt az élek megőrzése mellett:
from skimage.filters import median
from skimage.morphology import disk
def process_despeckle(image: np.ndarray, radius: int = 3) -> np.ndarray:
"""
Mediánszűrő alkalmazása pöttyösség csökkentésre.
Paraméterek:
image: Normalizált SAR kép (0-1 tartomány)
radius: Körkörös struktúra elem sugara (alapértelmezett: 3)
Visszatérési érték:
Zajszűrt kép
"""
despeckled = median(image, disk(radius))
return despeckled
# Eredeti és zajszűrt összehasonlítása
fig, axes = plt.subplots(1, 2, figsize=(14, 7))
axes[0].imshow(original, cmap='gray')
axes[0].set_title('Eredeti SAR kép')
axes[1].imshow(despeckled, cmap='gray')
axes[1].set_title(f'Zajszűrt (sugár={radius})')
plt.tight_layout()A Gray-Level Co-occurrence Matrix (GLCM) textúra leírókat számít ki:
from skimage.feature import graycomatrix, graycoprops
def compute_glcm_features(block: np.ndarray, levels: int = 16) -> dict:
"""
GLCM Haralick textúra jellemzők kiszámítása egy képblokkhoz.
Paraméterek:
block: 2D képblokk (uint8, 0-255 vagy szintekre skálázott)
levels: Szürkeségi szintek száma a GLCM-hez
Visszatérési érték:
Szótár kontraszt, homogenitás, energia, korreláció értékekkel
"""
# Skálázás a kívánt szintekre
block_scaled = ((block - block.min()) /
(block.max() - block.min() + 1e-8) * (levels-1)).astype(np.uint8)
# GLCM számítás
glcm = graycomatrix(block_scaled,
distances=[1],
angles=[0, np.pi/4, np.pi/2, 3*np.pi/4],
levels=levels,
symmetric=True,
normed=True)
# Haralick jellemzők kinyerése (átlag a szögeken)
features = {
'contrast': graycoprops(glcm, 'contrast').mean(),
'homogeneity': graycoprops(glcm, 'homogeneity').mean(),
'energy': graycoprops(glcm, 'energy').mean(),
'correlation': graycoprops(glcm, 'correlation').mean()
}
return features
def compute_texture_maps(image: np.ndarray, block_size: int = 16) -> dict:
"""
Textúra jellemző térképek számítása a teljes képre csúszó blokkokkal.
Paraméterek:
image: Normalizált SAR kép
block_size: Elemző blokkok mérete pixelben
Visszatérési érték:
2D textúra térképek szótára
"""
h, w = image.shape
h_blocks, w_blocks = h // block_size, w // block_size
# Térképek inicializálása
contrast_map = np.zeros((h_blocks, w_blocks))
homogeneity_map = np.zeros((h_blocks, w_blocks))
energy_map = np.zeros((h_blocks, w_blocks))
correlation_map = np.zeros((h_blocks, w_blocks))
img_uint8 = (image * 255).astype(np.uint8)
for i in range(h_blocks):
for j in range(w_blocks):
block = img_uint8[i*block_size:(i+1)*block_size,
j*block_size:(j+1)*block_size]
if block.max() > block.min():
features = compute_glcm_features(block)
contrast_map[i, j] = features['contrast']
homogeneity_map[i, j] = features['homogeneity']
energy_map[i, j] = features['energy']
correlation_map[i, j] = features['correlation']
return {
'contrast': contrast_map,
'homogeneity': homogeneity_map,
'energy': energy_map,
'correlation': correlation_map
}Sobel gradiensek és Canny éldetektálás struktúra elemzéshez:
from skimage.filters import sobel_h, sobel_v
from skimage.feature import canny
def process_edges(image: np.ndarray, sigma: float = 2.0) -> dict:
"""
Éldetektálás Sobel és Canny operátorokkal.
Paraméterek:
image: Normalizált SAR kép
sigma: Gauss simítás a Canny-hez
Visszatérési érték:
Gradiensek és éltérképek szótára
"""
# Sobel gradiensek
grad_x = sobel_h(image) # Vízszintes gradiens
grad_y = sobel_v(image) # Függőleges gradiens
# Gradiens nagyság
gradient_magnitude = np.sqrt(grad_x**2 + grad_y**2)
# Canny éldetektálás
edges = canny(image, sigma=sigma, low_threshold=0.05, high_threshold=0.15)
return {
'grad_x': grad_x,
'grad_y': grad_y,
'magnitude': gradient_magnitude,
'edges': edges
}
# Vizualizáció
fig, axes = plt.subplots(2, 2, figsize=(12, 12))
axes[0,0].imshow(image, cmap='gray')
axes[0,0].set_title('Eredeti')
axes[0,1].imshow(result['grad_x'], cmap='RdBu')
axes[0,1].set_title('Sobel X (vízszintes élek)')
axes[1,0].imshow(result['grad_y'], cmap='RdBu')
axes[1,0].set_title('Sobel Y (függőleges élek)')
axes[1,1].imshow(result['edges'], cmap='gray')
axes[1,1].set_title('Canny élek')Felügyelet nélküli textúra klaszterezés PCA vizualizációval:
from sklearn.cluster import MiniBatchKMeans
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
def extract_patch_features(patch: np.ndarray) -> np.ndarray:
"""
6D jellemzővektor kinyerése egy régióból.
Jellemzők: [átlag, szórás, kontraszt, homogenitás, energia, korreláció]
"""
# Intenzitás statisztikák
mean_i = patch.mean()
std_i = patch.std()
# GLCM jellemzők
patch_uint8 = (patch * 255).astype(np.uint8)
patch_scaled = ((patch_uint8 - patch_uint8.min()) /
(patch_uint8.max() - patch_uint8.min() + 1e-8) * 15).astype(np.uint8)
glcm = graycomatrix(patch_scaled, distances=[1], angles=[0],
levels=16, symmetric=True, normed=True)
contrast = graycoprops(glcm, 'contrast')[0, 0]
homogeneity = graycoprops(glcm, 'homogeneity')[0, 0]
energy = graycoprops(glcm, 'energy')[0, 0]
correlation = graycoprops(glcm, 'correlation')[0, 0]
return np.array([mean_i, std_i, contrast, homogeneity, energy, correlation])
def cluster_surface_units(image: np.ndarray,
patch_size: int = 32,
step: int = 16,
n_clusters: int = 5) -> dict:
"""
K-közép klaszterezés végrehajtása textúra régiókon.
Paraméterek:
image: Normalizált SAR kép
patch_size: Régiók mérete (pixel)
step: Lépésköz a régiók között
n_clusters: Klaszterek száma
Visszatérési érték:
Klasztertérkép, címkék és PCA koordináták szótára
"""
h, w = image.shape
patches = []
positions = []
# Régiók mintavételezése
for y in range(0, h - patch_size, step):
for x in range(0, w - patch_size, step):
patch = image[y:y+patch_size, x:x+patch_size]
patches.append(patch)
positions.append((y, x))
# Jellemzők kinyerése
features = np.array([extract_patch_features(p) for p in patches])
# Standardizálás
scaler = StandardScaler()
features_scaled = scaler.fit_transform(features)
# K-közép klaszterezés
kmeans = MiniBatchKMeans(n_clusters=n_clusters, random_state=42)
labels = kmeans.fit_predict(features_scaled)
# PCA vizualizációhoz
pca = PCA(n_components=2)
features_2d = pca.fit_transform(features_scaled)
# Klasztertérkép létrehozása
cluster_map = np.zeros((h, w))
for idx, (y, x) in enumerate(positions):
cluster_map[y:y+patch_size, x:x+patch_size] = labels[idx]
return {
'cluster_map': cluster_map,
'labels': labels,
'features_2d': features_2d,
'positions': positions,
'kmeans': kmeans,
'scaler': scaler,
'pca': pca
}Határok detektálása jellemzőtér-gradiensek alapján:
from scipy.ndimage import gaussian_filter
from skimage.transform import resize
def compute_boundary_map(image: np.ndarray,
window_size: int = 32,
step: int = 16) -> np.ndarray:
"""
Határ-valószínűség számítása textúra diszkontinuitás alapján.
Paraméterek:
image: Normalizált SAR kép
window_size: Elemzési ablak mérete
step: Ablak lépésköz
Visszatérési érték:
Határ-valószínűségi térkép (0-1)
"""
h, w = image.shape
n_y = (h - window_size) // step + 1
n_x = (w - window_size) // step + 1
# Jellemzők kinyerése minden ablakra
feature_grid = np.zeros((n_y, n_x, 6))
for i in range(n_y):
for j in range(n_x):
y, x = i * step, j * step
window = image[y:y+window_size, x:x+window_size]
feature_grid[i, j] = extract_patch_features(window)
# Jellemzők standardizálása
features_flat = feature_grid.reshape(-1, 6)
scaler = StandardScaler()
features_scaled = scaler.fit_transform(features_flat)
feature_grid_scaled = features_scaled.reshape(n_y, n_x, 6)
# Határ pontszámok számítása (távolság a szomszédoktól)
boundary_scores = np.zeros((n_y, n_x))
neighbors = [(-1, 0), (1, 0), (0, -1), (0, 1)]
for i in range(n_y):
for j in range(n_x):
feat = feature_grid_scaled[i, j]
distances = []
for dy, dx in neighbors:
ni, nj = i + dy, j + dx
if 0 <= ni < n_y and 0 <= nj < n_x:
neighbor_feat = feature_grid_scaled[ni, nj]
dist = np.linalg.norm(feat - neighbor_feat)
distances.append(dist)
if distances:
boundary_scores[i, j] = np.mean(distances)
# Normalizálás 0-1 tartományra
if boundary_scores.max() > boundary_scores.min():
boundary_scores = (boundary_scores - boundary_scores.min()) / \
(boundary_scores.max() - boundary_scores.min())
# Felskálázás és simítás
boundary_map = resize(boundary_scores, image.shape, order=1)
boundary_map = gaussian_filter(boundary_map, sigma=1.5)
return boundary_mapDomináns szerkezeti orientáció számítása struktúra tenzorral:
from skimage.filters import scharr_h, scharr_v
from scipy.ndimage import gaussian_filter
import matplotlib.colors as mcolors
def compute_orientation(image: np.ndarray,
sigma: float = 2.0) -> dict:
"""
Domináns orientáció számítása struktúra tenzorral.
Paraméterek:
image: Normalizált SAR kép
sigma: Simítás a struktúra tenzorhoz
Visszatérési érték:
Orientáció, koherencia és vizualizáció szótára
"""
# Zajszűrés először
image_smooth = median(image, disk(2))
# Gradiensek számítása (Scharr jobb forgási invarianciához)
Ix = scharr_h(image_smooth)
Iy = scharr_v(image_smooth)
# Struktúra tenzor komponensek simítással
Jxx = gaussian_filter(Ix * Ix, sigma=sigma)
Jyy = gaussian_filter(Iy * Iy, sigma=sigma)
Jxy = gaussian_filter(Ix * Iy, sigma=sigma)
# Orientációs szög
theta = 0.5 * np.arctan2(2 * Jxy, Jxx - Jyy)
# Sajátértékek a koherenciához
sqrt_term = np.sqrt((Jxx - Jyy)**2 + 4 * Jxy**2)
lambda1 = 0.5 * (Jxx + Jyy + sqrt_term)
lambda2 = 0.5 * (Jxx + Jyy - sqrt_term)
# Koherencia (anizotrópia mérték)
epsilon = 1e-10
coherence = (lambda1 - lambda2) / (lambda1 + lambda2 + epsilon)
# Alacsony energia régiók maszkolása
energy = lambda1 + lambda2
threshold = np.percentile(energy, 10)
mask = energy > threshold
coherence_masked = coherence * mask
# HSV vizualizáció: Árnyalat=orientáció, Érték=koherencia
hue = (theta + np.pi/2) / np.pi # Leképezés [0, 1]-re
sat = np.ones_like(hue)
val = coherence_masked
hsv = np.stack([hue, sat, val], axis=-1)
rgb = mcolors.hsv_to_rgb(hsv)
return {
'theta': theta,
'coherence': coherence_masked,
'rgb': rgb
}3D morfoszféra vizualizáció UMAP dimenziócsökkentéssel:
import umap
from skimage.feature import canny
def extract_8d_features(patch: np.ndarray) -> np.ndarray:
"""
8D jellemzővektor kinyerése morfoszféra elemzéshez.
Jellemzők: [átlag, szórás, kontraszt, homogenitás, energia, entrópia,
élsűrűség, orientációs_koherencia]
"""
# Alapstatisztikák
mean_i = patch.mean()
std_i = patch.std()
# GLCM jellemzők
patch_uint8 = (patch * 255).astype(np.uint8)
patch_scaled = ((patch_uint8 - patch_uint8.min()) /
(patch_uint8.max() - patch_uint8.min() + 1e-8) * 15).astype(np.uint8)
glcm = graycomatrix(patch_scaled, distances=[1], angles=[0],
levels=16, symmetric=True, normed=True)
contrast = graycoprops(glcm, 'contrast')[0, 0]
homogeneity = graycoprops(glcm, 'homogeneity')[0, 0]
energy = graycoprops(glcm, 'energy')[0, 0]
# Entrópia
glcm_flat = glcm[:, :, 0, 0].flatten()
glcm_flat = glcm_flat[glcm_flat > 0]
entropy = -np.sum(glcm_flat * np.log2(glcm_flat + 1e-10))
# Élsűrűség
edges = canny(patch, sigma=1.5)
edge_density = edges.mean()
# Orientációs koherencia
Ix = sobel_h(patch)
Iy = sobel_v(patch)
Jxx = gaussian_filter(Ix * Ix, sigma=1.5)
Jyy = gaussian_filter(Iy * Iy, sigma=1.5)
Jxy = gaussian_filter(Ix * Iy, sigma=1.5)
sqrt_term = np.sqrt((Jxx - Jyy)**2 + 4 * Jxy**2)
lambda1 = 0.5 * (Jxx + Jyy + sqrt_term)
lambda2 = 0.5 * (Jxx + Jyy - sqrt_term)
coherence = ((lambda1 - lambda2) / (lambda1 + lambda2 + 1e-10)).mean()
return np.array([mean_i, std_i, contrast, homogeneity,
energy, entropy, edge_density, coherence])
def create_morphospace(image: np.ndarray,
patch_size: int = 64,
step: int = 32,
n_clusters: int = 5) -> dict:
"""
3D morfoszféra létrehozása UMAP beágyazással.
Paraméterek:
image: Normalizált SAR kép
patch_size: Régióméret a jellemzőkinyeréshez
step: Lépésköz a régiók között
n_clusters: K-közép klaszterek száma
Visszatérési érték:
3D koordináták, jellemzők és klaszterek szótára
"""
h, w = image.shape
patches = []
positions = []
for y in range(0, h - patch_size, step):
for x in range(0, w - patch_size, step):
patch = image[y:y+patch_size, x:x+patch_size]
patches.append(patch)
positions.append((y, x))
# 8D jellemzők kinyerése
features = np.array([extract_8d_features(p) for p in patches])
# Standardizálás
scaler = StandardScaler()
features_scaled = scaler.fit_transform(features)
# UMAP 3D-be
reducer = umap.UMAP(n_components=3,
n_neighbors=15,
min_dist=0.1,
metric='euclidean',
random_state=42)
embedding_3d = reducer.fit_transform(features_scaled)
# K-közép klaszterezés
kmeans = MiniBatchKMeans(n_clusters=n_clusters, random_state=42)
labels = kmeans.fit_predict(features_scaled)
return {
'embedding': embedding_3d,
'features': features,
'labels': labels,
'positions': positions,
'patches': patches
}
# Interaktív 3D vizualizáció Plotly-val
import plotly.graph_objects as go
def plot_morphospace_3d(result: dict):
fig = go.Figure(data=[go.Scatter3d(
x=result['embedding'][:, 0],
y=result['embedding'][:, 1],
z=result['embedding'][:, 2],
mode='markers',
marker=dict(
size=4,
color=result['labels'],
colorscale='Viridis',
opacity=0.8
),
text=[f'Klaszter {l+1}' for l in result['labels']]
)])
fig.update_layout(
title='Venus SAR Textúra Morfoszféra',
scene=dict(
xaxis_title='UMAP 1',
yaxis_title='UMAP 2',
zaxis_title='UMAP 3'
)
)
return figPython csomagok az összes feldolgozási mód futtatásához:
# requirements.txt
numpy>=1.21.0
scipy>=1.7.0
scikit-image>=0.19.0
scikit-learn>=1.0.0
matplotlib>=3.5.0
umap-learn>=0.5.0
plotly>=5.0.0
Pillow>=9.0.0
requests>=2.27.0pip install -r requirements.txt
Color Legend:
Points are colored by texture cluster (1-5). Similar textures group together in 3D space. Clusters are determined by K-Means algorithm based on 8 texture features.